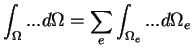Discrétisation par les éléments finis

Nous avons transformé les équations de départ pour obtenir une formulation intégrale faible en utilisant la méthode des résidus pondérés sous la forme dite de Galerkin. Nous allons procéder à la discrétisation de ce problème avec la méthode des éléments finis.
La méthode des éléments finis utilise des fonctions d'approximation de la solution recherchée.
Afin que ces fonctions aient des formes simples, l'approximation est définie au niveau de sous domaines formant une partition du domaine $\Omega$. Ces sous domaines, appelés éléments finis, auront des formes géométriques simples.
Partant d'une formulation intégrale, la discrétisation s'écrit simplement :

$$\int_\Omega ... d\Omega = \sum_e \int_{\Omega_e} ... d\Omega_e$$

Cependant pour que cette égalité soit vraie il faut les fonctions qui apparaissent dans l'intégrale vérifient la propriété suivante :

S'il existe dans la formulation intégrale des dérivées des fonctions

à l'ordre m, il faut que leurs dérivées à l'ordre m-1 soient

continues aux frontières des éléments de la discrétisation.

Si cette propriété n'est pas vérifiée il y a des termes supplémentaires issus des frontières des éléments.

$$\int_\Omega ... d\Omega = \sum_e \int_{\Omega_e} ... d\Omega_e + \sum_e \int_{\Gamma_e} ... d\Gamma_e$$

Exemple : si une fonction $\phi$ n'est pas continue à la frontière des éléments ses dérivées ne sont pas finies sur ces frontières. Il faudrait alors construire une méthode qui permette de borner $\int_{\Gamma_e} \frac{\partial \phi}{\partial x} d\Gamma_e$.
Il est possible de construire des méthodes d'éléments finis sous cette forme ; ce n'est pas, cependant, le cas le plus courant.
La règle énoncée ci-dessus appliquée à la formulation faible de l'équation de Poisson implique la continuité des fonctions d'approximation aux frontières des éléments (du fait de la présence de dérivées d'ordre un) ; la forme initiale aurait nécessité la continuité des dérivées premières.
Convergence de l'approximation : comme pour toutes méthodes de discrétisation, il faut que la solution approchée tende vers la solution exacte quand on fait tendre la taille des éléments finis vers zéro.
La condition de continuité imposée aux fonctions d'approximation est une des conditions qui assurent la convergence de la méthode. Lorsque cette condition est vérifiée on dit que les éléments finis sont conformes. Dans le cas contraire (éléments finis non conformes) il faut s'assurer que les termes issus des frontières entre les éléments tendent vers zéro quand la taille des éléments tend vers zéro.
L'autre condition nécesssaire à la convergence de l'approximation est la suivante :

Il faut que l'approximation utilise une base polynomiale complète

jusqu'à l'ordre m s'il y a des dérivées d'ordre m dans la

formulation.

Considérons l'approximation de u suivante :

 

$$u_{app} (\overrightarrow{x}) = \sum_i a_i f_i (\overrightarrow{x})$$ (5.1)

$f_i (\overrightarrow{x})$	: fonctions de forme connues
ai	: coefficients

• Pour que
  
  $$\vert u_{app} - u\vert \rightarrow 0$$
  
  
  quand la taille des éléments tend vers 0 il faut que le développement 5.1 contienne un terme constant.
• Pour que
  
  $$\left\vert\frac{\partial u_{app}}{\partial x} - \frac{\partial u}{\partial x}\right\vert \rightarrow 0$$
  
  
  quand la taille des éléments tend vers 0 il faut que le développement 5.1 contienne un terme en x.
• etc...