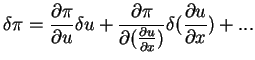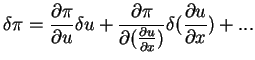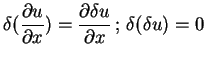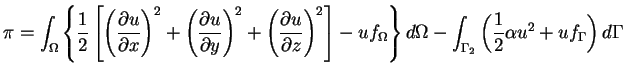Next: Discrétisation par les éléments
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: Formulation faible
Afin d'introduire la méthode de Galerkin, telle qu'elle a été conçue à l'origine, on va se placer dans un contexte fonctionnel :
Soit une fonctionnelle
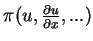 ,
sa première variation s'écrit :
,
sa première variation s'écrit :
où 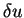 est une variation quelconque de u.
est une variation quelconque de u.
On rappelle quelques propriétés des calculs variationnels :
Il est possible, dans certains cas simples, de construire une fonctionnelle 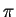 telle qu'écrire
telle qu'écrire
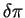 =0 soit équivalent au problème à résoudre.
=0 soit équivalent au problème à résoudre.
Exemple : l'équation de Poisson
 est équivalent à 3.1 avec
est équivalent à 3.1 avec
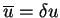 .
.
Dans la méthode de Galerkin les fonctions de pondération sont représentées par les variations de la fonction inconnue u.
On notera que le choix de fonctions de pondération nulles aux endroits où la fonction u est imposée consiste ici à considérer que la variation est nulle lorsque u est connue.
Dans la méthode de Galerkin les fonctions de pondération appartiennent au même espace que les fonctions inconnues u (ceci est vrai aussi bien pour un espace continu que pour un espace discret).
D'une façon plus générale, on appelle méthode de Galerkin les méthodes des résidus pondérés pour lesquelles on a les propriétés suivantes :
- les espaces des fonctions inconnues et des fonctions de pondération sont les mêmes,
- les fonctions de pondération sont nulles lorsque les fonctions inconnues sont imposées,
et cela même s'il n'existe pas de fonctionnelle 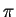 telle que
telle que
 soit équivalent à la formulation intégrale du problème posé.
soit équivalent à la formulation intégrale du problème posé.




Next: Discrétisation par les éléments
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: Formulation faible
Marc Grandotto
2001-11-29