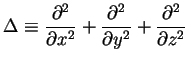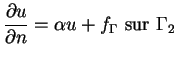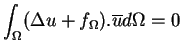Next: Formulation faible
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: Historique des applications de
On considère un domaine 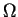 et sa frontière
et sa frontière 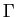 .
.
Figure:
Domaine 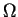
|
|
Soit un système d'équations aux dérivées partielles (EDP) d'ordre m (m est l'ordre maximal des dérivées présentes dans les équations) :
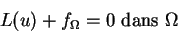 |
(2.1) |
Auquel sont associées les conditions aux limites suivantes :
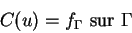 |
(2.2) |
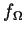 |
: fonction connue dans 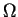 |
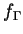 |
: fonction connue sur 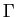 |
| u |
: fonction inconnue |
Ce sont des fonctions des coordonnées de l'espace.
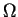 est un espace ouvert borné de
est un espace ouvert borné de
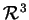 .
.
On appelle résidu la quantité suivante :
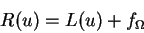 |
(2.3) |
Si u est solution de 2.1 alors R(u)=0.
La méthode des résidus pondérés est la recherche des fonctions u telles que l'intégrale suivante soit nulle :
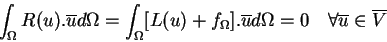 |
(2.4) |
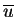 : fonctions de pondération appartenant à un espace de fonctions
: fonctions de pondération appartenant à un espace de fonctions
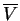 .
.
Les fonctions u appartiennent à un espace de fonctions noté V. Ces fonctions vérifient les conditions aux limites 2.2 et sont dérivables m fois.
Théorème :
Si 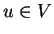 vérifie 2.4
vérifie 2.4
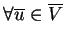 alors u vérifie 2.1.
alors u vérifie 2.1.
Démonstration : supposons
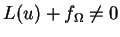 ,
alors il est possible de choisir une fonction
,
alors il est possible de choisir une fonction
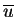 telle que
telle que
![$\int_{\Omega}[L(u)+f_{\Omega}].\overline{u} d\Omega \neq 0$](img16.gif) .
.
La méthode des résidus pondérés permet donc une formulation intégrale d'un problème.
Le nom de formulation variationnelle provient du fait que l'on peut aussi, dans certains cas simples, obtenir une formulation intégrale à partir de la notion de fonctionnelle en utilisant un principe de stationnarité (on y reviendra plus loin) ; mais ce n'est alors qu'un cas particulier de la méthode des résidus pondérés qui a une plus grande portée.
Remarques :
- Un espace continu est un espace qui a un nombre infini de degrés de liberté.
- Un espace discret est un espace qui a un nombre fini de degrés de liberté.
- Si V et
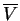 sont des espaces continus on aura la solution en tous points de
sont des espaces continus on aura la solution en tous points de 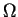 (exemple : une solution analytique).
(exemple : une solution analytique).
- Si V et
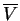 sont des espaces discrets on n'aura la solution qu'en certains points de
sont des espaces discrets on n'aura la solution qu'en certains points de 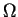 (les points de la discrétisation).
(les points de la discrétisation).
- Les solutions analytiques étant exceptionnelles, c'est sous la forme discrète que l'on va utiliser la méthode des résidus pondérés.
Exemple : l'équation de Poisson
Conditions aux limites :
- Dirichlet (valeurs imposées) : u=ud sur
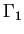 .
.
- Neumann-Cauchy (dérivées normales imposées) :
Application de la méthode des résidus pondérés :
u est une fonction dérivable deux fois, on a une équation d'ordre deux.




Next: Formulation faible
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: Historique des applications de
Marc Grandotto
2001-11-29
![\includegraphics[width=7cm]{omega.eps}](img3.gif)