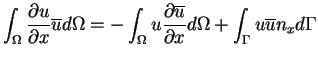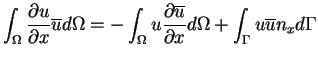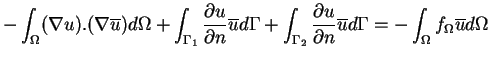Formulation faible

On cherche à diminuer les contraintes de dérivabilité imposées aux fonctions u. Pour cela on utilise l'intégration par partie :

$$\int_{\Omega}\frac{\partial u}{\partial x}\overline{u}d\Omega = -... ...\partial \overline{u}}{\partial x}d\Omega+\int_{\Gamma}u\overline{u}n_x d\Gamma$$

Exemple : l'équation de Poisson

$$-\int_{\Omega}(\nabla u).(\nabla\overline{u})d\Omega +\int_{\Gamm... ...}{\partial n}\overline{u} d\Gamma = -\int_{\Omega}f_{\Omega}\overline{u}d\Omega$$

En choisissant des fonctions de pondération nulles sur 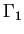$\Gamma_1$ et en utilisant la condition aux limites sur 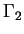$\Gamma_2$ on obtient :

 

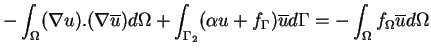$$-\int_{\Omega}(\nabla u).(\nabla\overline{u})d\Omega +\int_{\Gamm... ...u+f_{\Gamma})\overline{u} d\Gamma = -\int_{\Omega}f_{\Omega}\overline{u}d\Omega$$ (3.1)

avec u=u_d sur 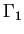$\Gamma_1$.
Les contraintes imposées aux fonctions sont les suivantes :

• u et 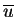$\overline{u}$ doivent être dérivables une fois; il faut aussi que le carré de leurs dérivées soit intégrable : on dit que ce sont des fonctions dont les dérivées sont de carré sommable et les espaces auxquels appartiennent de telles fonctions sont appelés espaces de Sobolev.
• u vérifie les conditions de Dirichlet.
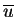• $\overline{u}$=0 sur les parties de la frontières où u est imposée (conditions de Dirichlet).

On observe que les conditions de Neumann-Cauchy sont incluses dans l'équation : on dit que ces conditions sont naturelles dans la formulation faible.