Conditions aux limites de Dirichlet

Les conditions de Neumann-Cauchy ont été prises en compte par la formulation et sont représentées par des termes assemblés dans le système algébrique. La prise en compte des conditions de Dirichlet intervient au niveau du système algébrique.
Lorsqu'on construit le système algébrique il y a autant de lignes que d'inconnues 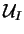${\cal U}_I$ ; autrement dit il y a autant d'équations que d'inconnues, à chaque noeud est associée une équation par l'intermédiaire de la fonction de pondération. Une condition de Dirichlet signifie qu'en certains noeuds de la frontière la valeur de 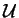${\cal U}$ est fixée, donc connue ; on n'a donc pas besoin des équations qui sont associées à ces noeuds et il faut les éliminer du système algébrique ; cela se fait en supprimant les lignes correspondantes dans le système. C'est la traduction concrète du choix de fonctions de pondération nulles associées aux noeuds Dirichlet.
On peut réaliser cela par deux méthodes.