



Next: Méthode par élimination effective
Up: Conditions aux limites de
Previous: Conditions aux limites de
On assemble le système algébrique sans tenir compte des conditions de Dirichlet, c.a.d. avec toutes les lignes. Ensuite, pour les noeuds pour lesquels la fonction u est connue on va introduire la valeur imposée de la façon suivante : on ajoute un nombre 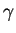 aux termes diagonaux correspondants aux noeuds Dirichlet et on remplace les seconds membres correspondants par le produit de la valeur imposée par
aux termes diagonaux correspondants aux noeuds Dirichlet et on remplace les seconds membres correspondants par le produit de la valeur imposée par 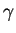 .
Il faut que
.
Il faut que 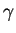 soit grand par rapport aux valeurs des
soit grand par rapport aux valeurs des
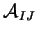 .
L'équation associée à un noeud Dirichlet I s'écrit :
.
L'équation associée à un noeud Dirichlet I s'écrit :
Elle conduit à :
 si
si
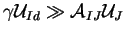 .
.
En pratique on prend
 ou
ou
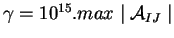
La valeur de 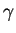 dépend de la précision de la représentation des nombres dans l'ordinateur utilisé. Cette méthode est facile à mettre en oeuvre mais elle est limitée lorsque les termes du système algébrique sont grands. De plus elle ne diminue pas la taille du système à résoudre.
dépend de la précision de la représentation des nombres dans l'ordinateur utilisé. Cette méthode est facile à mettre en oeuvre mais elle est limitée lorsque les termes du système algébrique sont grands. De plus elle ne diminue pas la taille du système à résoudre.
Marc Grandotto
2001-11-29