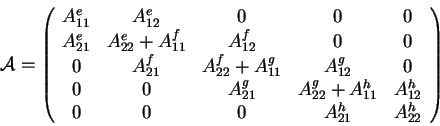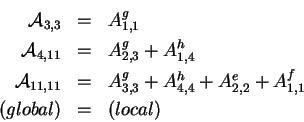Système algébrique global, assemblage

La constitution du système algébrique global, dont le résolution conduira à la solution du problème, s'appelle l'assemblage. Cela consiste à réaliser la somme sur les éléments. On utilise pour cela la connectivité :

$$\begin{eqnarray*}\sum_e A^e_{ij} u_j = \sum_e F^e_i \mbox{ devient } {\cal A}_{I... ...l F}_I \\ \mbox{avec } I=CONNEC(i,e) \mbox{ et } J=CONNEC(j,e) \end{eqnarray*}$$

Exemple monodimensionnel :

 

Figure 13.1: Maillage 1D

$${\cal A} = \left( \begin{array}{ccccc} A^e_{11} & A^e_{12} & ... ...^h_{12} \\ 0 & 0 & 0 & A^h_{21} & A^h_{22} \end{array}\right)$$

Exemple bidimensionnel :

 

Figure 13.2: Maillage 2D

$$\begin{eqnarray*}{\cal A}_{3,3} & = & A^g_{1,1} \\ {\cal A}_{4,11} & = & A^g_{2... ... + A^h_{4,4} + A^e_{2,2} + A^f_{1,1} \\ (global) & = & (local) \end{eqnarray*}$$