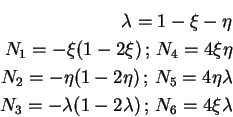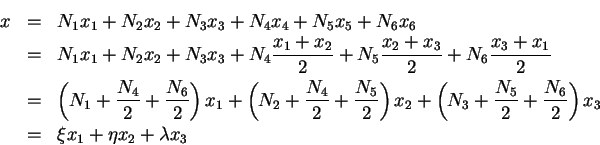Passage de l'élément de référence vers les éléments du maillage

Soit l'espace de référence 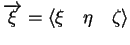$\overrightarrow{\xi} = \langle \xi \quad \eta \quad \zeta \rangle$ et l'espace du maillage 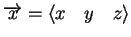$\overrightarrow{x} = \langle x \quad y \quad z \rangle$, on considère la transformation géométrique suivante :

$$\tau \quad : \quad \overrightarrow{\xi}\longmapsto \overrightarrow{x} = \overrightarrow{x}(\overrightarrow{\xi})$$

$$\tau^{-1} \quad : \quad \overrightarrow{x}\longmapsto \overrightarrow{\xi} = \overrightarrow{\xi}(\overrightarrow{x})$$

On a :

$$\overrightarrow{x}(\overrightarrow{\xi}) = \sum_i \overrightarrow{x_i} \tilde{N_i} (\overrightarrow{\xi})$$

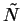$\tilde{N}$ désigne les fonctions permettant la transformation géométrique. Lorsque 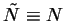$\tilde{N} \equiv N$ on a des éléments isoparamétriques. Lorsque le degré des polynômes de 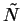$\tilde{N}$ est inférieur à celui des des polynômes de N on a des éléments sous paramétriques.
Exemple : sous paramétricité de l'élément P2
On considère un triangle à cotés droits et une approximation quadratique (note : il existe égalemment un triangle dont les cotés sont des arcs de parabole, mais il n'a pas la propriété d'être sous paramétrique).

 

Figure 9.1: Elément P2

Les fonctions d'approximations sont :

$$\begin{eqnarray*}\lambda = 1 - \xi - \eta \nonumber \\ N_1 = -\xi (1 - 2 \xi) \... ...\ N_3 = -\lambda (1 - 2 \lambda) \mbox{ ; } N_6 = 4 \xi \lambda \end{eqnarray*}$$

$$\begin{eqnarray*}x & = & N_1 x_1 + N_2 x_2 + N_3 x_3 + N_4 x_4 + N_5 x_5 + N_6 x... ...{N_6}{2} \right) x_3 \\ & = & \xi x_1 + \eta x_2 + \lambda x_3 \end{eqnarray*}$$