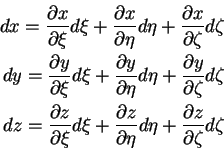Next: Application à l'équation de
Up: Passage de l'élément de
Previous: Transformation des dérivées
 désigne l'élément de référence.
désigne l'élément de référence.
En effet on a :
 ,
avec
,
avec
 ,
,
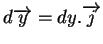 ,
,
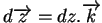 ,
où
,
où
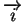 ,
,
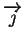 ,
,
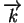 sont les vecteurs unitaires d'un repère cartésien orthonormé.
sont les vecteurs unitaires d'un repère cartésien orthonormé.
Donc

En exprimant  dans l'espace de référence on a :
dans l'espace de référence on a :
 ,
et comme :
,
et comme :
on en déduit que
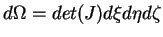 .
.
Commentaire :
Pour 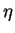 et
et  constants on a :
constants on a :
dx,dy,dz sont les composantes d'un vecteur pour lequel 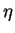 et
et  sont constants.
sont constants.
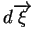 est un vecteur tangent à (
est un vecteur tangent à (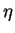 et
et  constants), c'est à dire parallèle au vecteur précédent, il a donc les mêmes composantes :
constants), c'est à dire parallèle au vecteur précédent, il a donc les mêmes composantes :
Marc Grandotto
2001-11-29