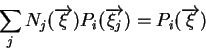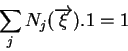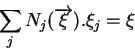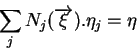Next: Passage de l'élément de
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: L'élément de référence
Dans ce qui suit
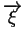 est un vecteur de composantes
est un vecteur de composantes

- On choisit une base polynomiale, par exemple :
- On cherche une approximation de la forme :
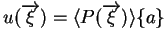 |
|
|
(8.1) |
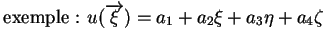 |
|
|
|
- On évalue la matrice nodale en écrivant que les valeurs nodales de u sont les valeurs prises par l'approximation aux noeuds de la discrétisation :
Exemple :
- On inverse la matrice nodale (elle ne doit pas être singulière) :
![$\displaystyle \{a\} = {[P]}^{-1} \{u\}$](img70.gif) |
|
|
(8.2) |
- On calcule alors les fonctions N : on veut que
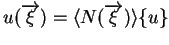 ; en utilisant 8.1, puis 8.2, on obtient :
; en utilisant 8.1, puis 8.2, on obtient :
![$\displaystyle u(\overrightarrow{\xi}) = \langle P(\overrightarrow{\xi})\rangle \{ a \} = \langle P(\overrightarrow{\xi})\rangle {[P]}^{-1} \{u\}$](img72.gif) |
|
|
|
![$\displaystyle \mbox{c.a.d. } \langle N(\overrightarrow{\xi})\rangle = \langle P(\overrightarrow{\xi})\rangle {[P]}^{-1}$](img73.gif) |
|
|
(8.3) |
Exemple monodimensionnel :
En multipliant 8.3 par [P] on obtient :
c.a.d.
On a ainsi :
Ces relations permettent de vérifier que les fonctions d'approximation forment bien une base polynomiale complète à l'ordre voulu.




Next: Passage de l'élément de
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: L'élément de référence
Marc Grandotto
2001-11-29
![\begin{displaymath}\left\{
\begin{array}{c} u_1 \\ u_2 \\ . \\ u_n \end{array} \...
...i_n) & P_2(\xi_n) & . & P_n(\xi_n) \end{array} \right]
\{ a \}
\end{displaymath}](img67.gif)
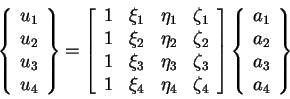
![\begin{displaymath}\left\{
\begin{array}{c} u_1 \\ u_2 \\ . \\ u_n \end{array} \...
...i_n) & P_2(\xi_n) & . & P_n(\xi_n) \end{array} \right]
\{ a \}
\end{displaymath}](img67.gif)
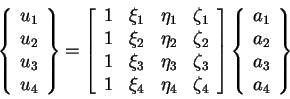
![\begin{displaymath}\langle P(\xi)\rangle = \langle 1 \quad \xi \rangle \mbox{ ; ...
... =
\left[ \begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \right] \end{displaymath}](img74.gif)
![\begin{displaymath}{[P]}^{-1} = \left[ \begin{array}{cc} 1 & 0 \\ -1 & 1 \end{ar...
...e \left[ \begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array} \right] \end{displaymath}](img75.gif)