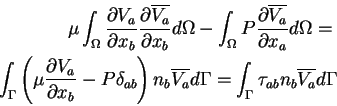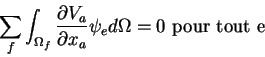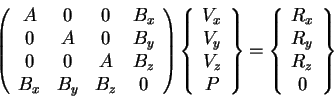Next: Equations de Navier-Stokes
Up: Introduction aux problèmes de
Previous: Introduction aux problèmes de
Les équations du problème de Stokes régissent l'écoulement laminaire, isotherme, incompressible et stationnaire d'un fluide visqueux à viscosité constante pour lequel le terme de convection a été négligé. C'est un problème modèle pour l'étude de la discrétisation des équations de la mécanique des fluides.
On utilise la sommation sur les indices répétés.
- Equation de conservation de la masse :
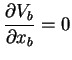 |
|
|
(18.1) |
- Equation de conservation de la quantité de mouvement :
V est la vitesse (m/s), P est la pression (Pa) et 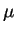 est la viscosité moléculaire (kg/m.s).
est la viscosité moléculaire (kg/m.s).
On a un système à deux équations dont l'une est scalaire (18.1) et l'autre est vectorielle (18.2). On a deux inconnues, la pression qui est un scalaire et la vitesse qui est un vecteur.
Dans la suite de l'étude on ne retiendra que la partie symétrique du tenseur des contraintes 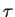 car,
car, 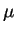 étant constante et l'écoulement étant incompressible, on peut écrire :
étant constante et l'écoulement étant incompressible, on peut écrire :
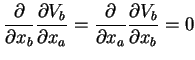 |
|
|
|
 |
|
|
(18.3) |
L'application de la méthode des résidus pondérés aux équations 18.1 et 18.3 s'écrit :
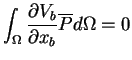 |
|
|
(18.4) |
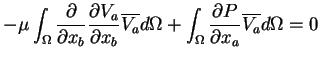 |
|
|
(18.5) |
L'intégration par partie de 18.5 (formulation faible) s'écrit :
On a utilisé deux fonctions de pondération, la fonction de pondération scalaire
 associée à l'équation scalaire 18.1 et la fonction de pondération vectorielle
associée à l'équation scalaire 18.1 et la fonction de pondération vectorielle
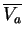 associée à l'équation vectorielle 18.3.
associée à l'équation vectorielle 18.3.
L'intégration par partie porte sur le terme diffusif et sur le gradient de pression.
L'analyse des contraintes de continuité montre qu'il faut utiliser des fonctions d'approximation continues, polynomiale d'ordre au moins égal à un pour la vitesse et sa fonction de pondération. Il n'y a pas de contrainte particulière concernant la pression et sa fonction de pondération.
Cela nous conduit au choix suivant : l'approximation de la vitesse, ou plus précisemment de chaque composante de la vitesse, est la même que celle utilisée pour la fonction u de l'équation de Poisson ; l'approximation de la pression est obtenue en utilisant la projection élémentaire, c.a.d par les fonctions discontinues et constantes par élément.
L'approximation choisie pour
 permet de vérifier la conservation de la masse au niveau de chaque élément. En effet, les fonctions de la procjection élémentaire sont telles qu'elles valent 1 dans l'élément auquel elles sont associées et 0 dans les autres. 18.4 devient :
permet de vérifier la conservation de la masse au niveau de chaque élément. En effet, les fonctions de la procjection élémentaire sont telles qu'elles valent 1 dans l'élément auquel elles sont associées et 0 dans les autres. 18.4 devient :
Commentaire :
Le choix d'une base de fonctions constantes par élément pour
 conduit à :
conduit à :
La discrétisation du domaine  donne :
donne :
Comme, par définition de la base on a
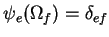 ,
on obtient :
,
on obtient :
Ce choix de fonctions de pondération est égalemment celui qui est fait pour obtenir une formulation "volumes finis" :
devient :
et en utilisant le théorème de la divergence on obtient le bilan des flux sur les faces des volumes :
La discrétisation fait apparaitre les matrices élémentaires suivantes :
On peut alors écrire le système algébrique suivant :
ou encore, afin de faire apparaitre l'assemblage :
pour tout a = x,y,z.
Les conditions aux limites associées aux équations du problème de Stokes (elles sont aussi valable pour les équations de Navier-Stokes) sont :
- Conditions de Dirichlet : composantes de la vitesse imposées.
- Condition de Neumann :
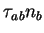 imposé (il s'agit d'une force).
imposé (il s'agit d'une force).
Il est plus commode d'exprimer les conditions aux limites dans les repères locaux associés aux frontières un utilisant les rotations permettant de passer du repère général (x, y, z) aux repères locaux dits "tangent-normal" (t1, t2, n) où t1 et t2 sont les tangentes à la frontière et n est la normale à la frontière dirigée vers l'extérieur du domaine. Dans le cas bidimensionnel, les conditions de Neumann s'écrivent alors :
- Condition associée à l'équation de Vn :
- Condition associée à l'équation de Vt :
Du point de vue de la mécanique des fluides une condition de glissement ou de symétrie s'écrit :
et une condition de régime établi s'écrit :
On notera que la pression intervient dans les conditions aux limites par l'intermédiaire des conditions de Neumann portant sur la vitesse normale.




Next: Equations de Navier-Stokes
Up: Introduction aux problèmes de
Previous: Introduction aux problèmes de
Marc Grandotto
2001-11-29