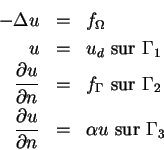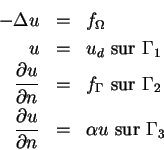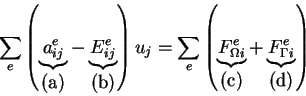Système algébrique élémentaire

On va utiliser l'exemple de l'équation de Poisson.

$$\begin{eqnarray*}- \Delta u & = & f_\Omega \\ u & = & u_d \mbox{ sur } \Gamma_1... ...rac{\partial u}{\partial n} & = & \alpha u \mbox{ sur } \Gamma_3 \end{eqnarray*}$$

En utilisant les matrices et les vecteurs élémentaires définis précédemment on obtient :

$$\begin{eqnarray*}\sum_e \left( \underbrace{a^e_{ij}}_{\mbox{(a)}} - \underbrace{... ..._{\mbox{(c)}} + \underbrace{F^e_{\Gamma i}}_{\mbox{(d)}} \right) \end{eqnarray*}$$

(a)	: Laplacien
(b)	: Condition de Cauchy
(c)	: Source
(d)	: Condition de Neumann