Cas général

On utilise une méthode d'intégration numérique dont la forme générale peut s'écrire :

$$\begin{eqnarray*}\int_{\hat{\Omega}} f(\xi) d\hat{\Omega} = \sum_k f(\xi_k) w_k \end{eqnarray*}$$

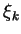$\xi_k$ et w_k sont respectivement les points et les poids associés à la méthode d'intégration.
Les méthodes les plus courantes sont la méthode de Hammer pour les triangles et les tétraèdres et la méthode de Gauss pour les quadrilatères et les hexaèdres.
La précision des calculs est d'autant plus grande que le nombre de points d'intégration est grand. Il apparait donc ici une nouvelle source d'erreur dans l'approximation. Cela a aussi une incidence sur le coût des calculs.
On rappelle qu'une méthode de Gauss à n points (à une dimension) permet d'intégrer exactement les polynômes de degré inférieur ou égal à 2n-1. C'est la méthode la plus précise pour un nombre de points donné.
Les points et les poids des méthodes d'intégration se trouvent facilement dans la littérature.
A plusieurs dimension on désigne les méthodes d'intégration par leur nombre de points équivalent à une dimension (exemple : méthode de Gauss à 2x2 points).
Lorsque le Jacobien est une fonction de l'espace, l'intégration n'est jamais exacte en présence de dérivées car on doit intégrer des fractions rationnelles (inverse du Jacobien).