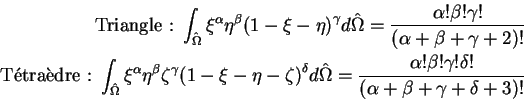Cas des éléments affines

On appelle éléments affines les éléments pour lesquels le Jacobien J est indépendant de 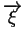$\overrightarrow{\xi}$. C'est par exemple le cas pour le triangle et le tétraèdre linéaires.
Dérivées des fonctions du triangle :

$$\begin{eqnarray*}\frac{\partial N_1}{\partial \xi} = 1 \mbox{ ; } \frac{\partial... ...ial \eta} = 1 \mbox{ ; } \frac{\partial N_3}{\partial \eta} = -1 \end{eqnarray*}$$

Il est alors possible de précalculer exactement les intégrales apparaissant dans les matrices et les vecteurs élémentaires. Il s'agit en effet d'intégrales de produits de polynômes pour lesquelles on dispose de formules appropriées :

$$\begin{eqnarray*}\mbox{Triangle : } \int_{\hat{\Omega}} \xi^\alpha \eta^\beta {(... ...ta ! \gamma ! \delta !}{(\alpha + \beta + \gamma + \delta + 3)!} \end{eqnarray*}$$