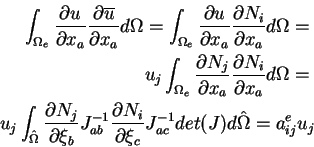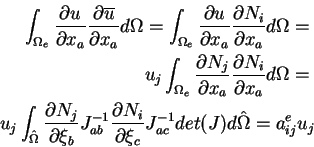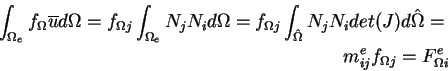Next: Calcul des intégrales
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: Transformation des intégrales
La formulation intégrale est vraie
 (méthode des résidus pondérés), elle est donc vraie pour toutes les fonctions d'approximation N. Les fonctions N constituent une base de l'espace des fonctions u et
(méthode des résidus pondérés), elle est donc vraie pour toutes les fonctions d'approximation N. Les fonctions N constituent une base de l'espace des fonctions u et
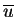 .
.
Dans ce qui suit on utilise la sommation sur les indices répétés.
ae est une matrice élémentaire.
Pour le second membre (terme source), si 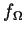 est donné par noeud, on a :
est donné par noeud, on a :
me est une autre matrice élémentaire,
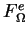 est un vecteur élémentaire.
est un vecteur élémentaire.
si 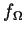 est donné par élément, on a :
est donné par élément, on a :
Remarque : On a utilisé deux projections discrètes différentes (par noeud ou par élément) pour la fonction connue 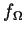 .
Il est important de noter que, lorsqu'on résoud un problème par discrétisation, toutes les informations doivent être projetées dans les espaces d'approximation utilisés. Si la fonction
.
Il est important de noter que, lorsqu'on résoud un problème par discrétisation, toutes les informations doivent être projetées dans les espaces d'approximation utilisés. Si la fonction 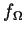 est connue dans tout le domaine
est connue dans tout le domaine 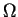 (donnée analytique), et comme elle n'apparait pas dans une dérivée, on a le choix de la projeter soit dans l'espace des fonctions u (fonctions continues, projection nodale), soit dans l'espace des fonctions constantes par élément (fonctions discontinues, projection élémentaire). Le critère de choix dépend de la précision recherchée ; si la variation spatiale de la fonction est importante la projection nodale sera plus précise. Un autre critère doit être pris en compte, il s'agit du coût des calculs : la projection nodale demande plus d'opérations que la projection élémentaire. On verra plus loin une autre projection fréquemment rencontrée qui est liée à la méthode utilisée pour le calcul des intégrales.
(donnée analytique), et comme elle n'apparait pas dans une dérivée, on a le choix de la projeter soit dans l'espace des fonctions u (fonctions continues, projection nodale), soit dans l'espace des fonctions constantes par élément (fonctions discontinues, projection élémentaire). Le critère de choix dépend de la précision recherchée ; si la variation spatiale de la fonction est importante la projection nodale sera plus précise. Un autre critère doit être pris en compte, il s'agit du coût des calculs : la projection nodale demande plus d'opérations que la projection élémentaire. On verra plus loin une autre projection fréquemment rencontrée qui est liée à la méthode utilisée pour le calcul des intégrales.




Next: Calcul des intégrales
Up: ÉCOLE SUPÉRIEURE D'INGÉNIEURS DE
Previous: Transformation des intégrales
Marc Grandotto
2001-11-29