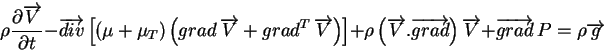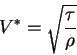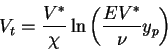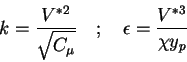Next: About this document ...
Up: Introduction aux problèmes de
Previous: Equations de Navier-Stokes
On se place dans le cas isotherme. Les équations de Navier-Stokes décriventl'évolution des valeurs instantannées de la vitesse et de la pression. Lorsque le nombre de Reynolds (
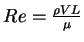 ,
où L est une longueur caractéristique) est plus grand qu'une valeur critique (de l'ordre de 1000) l'écoulement devient turbulent, c.a.d. que la vitesse et la pression fluctuent rapidemment avec le temps. Il est rarement possible, dans le cas turbulent, de résoudre les équations des valeurs instantannées. On décompose alors les valeurs instantannées en valeurs moyennes et en fluctuations.
,
où L est une longueur caractéristique) est plus grand qu'une valeur critique (de l'ordre de 1000) l'écoulement devient turbulent, c.a.d. que la vitesse et la pression fluctuent rapidemment avec le temps. Il est rarement possible, dans le cas turbulent, de résoudre les équations des valeurs instantannées. On décompose alors les valeurs instantannées en valeurs moyennes et en fluctuations.
On fait ensuite la moyenne des équations des valeurs instantannées pour obtenir les équations des valeurs moyennes. Celles-ci sont similaires aux équations de Navier-Stokes mais contiennent le terme supplémentaire suivant (dû au terme convectif) :
On relie ce terme aux quantités moyennes par la modélisation suivante :
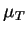 est la viscosité turbulente.
est la viscosité turbulente.
L'équation de la quantité de mouvement moyenne, appelée équation de Reynolds s'écrit :
La fermeture du système nécessite la détermination de 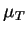 .
.
On utilise assez couramment le modèle
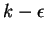 ,
qui consiste à relier
,
qui consiste à relier 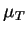 à l'énergie cinétique de la turbulence (k) et à sa dissipation (
à l'énergie cinétique de la turbulence (k) et à sa dissipation (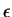 )
pour lesquelles on peut établir les équations suivantes :
)
pour lesquelles on peut établir les équations suivantes :
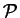 est la production d'énergie cinétique de la turbulence k.
est la production d'énergie cinétique de la turbulence k.
Les quantités 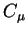 ,
,
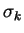 ,
,
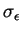 ,
,
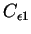 et
et
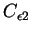 sont les constantes du modèle
sont les constantes du modèle
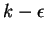 .
Leurs valeurs sont
.
Leurs valeurs sont
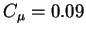 ,
,
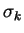 =1.0,
=1.0,
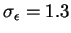 ,
,
 et
et
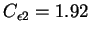
On notera que les équations de k et de 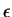 sont des équations de diffusion-convection qui ne présentent pas de difficulté particulière en ce qui concerne leur discrétisation par éléments finis.
sont des équations de diffusion-convection qui ne présentent pas de difficulté particulière en ce qui concerne leur discrétisation par éléments finis.
Par contre ces équations (quantité de mouvement moyenne, k, 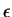 )
nécessitent des conditions aux limites spéciales sur les parois solides. Cette modélisation n'est en effet pas valable près des parois. On utilise la technique des lois de parois qui consiste, entre autre, à relier le cisaillement moyen à la vitesse moyenne par une loi analytique.
)
nécessitent des conditions aux limites spéciales sur les parois solides. Cette modélisation n'est en effet pas valable près des parois. On utilise la technique des lois de parois qui consiste, entre autre, à relier le cisaillement moyen à la vitesse moyenne par une loi analytique.
Soit 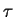 le cisaillement moyen à la paroi, Vt la vitessse tangentielle moyenne à une distance yp de la paroi, on définit la vitesse de frottement :
le cisaillement moyen à la paroi, Vt la vitessse tangentielle moyenne à une distance yp de la paroi, on définit la vitesse de frottement :
Les lois de parois s'écrivent :
Avec la constante de Von Karman 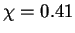 et la rugosité E=9.
et la rugosité E=9.
Ces lois sont valables pour
 compris entre 100. et 1000.
compris entre 100. et 1000.




Next: About this document ...
Up: Introduction aux problèmes de
Previous: Equations de Navier-Stokes
Marc Grandotto
2001-11-29