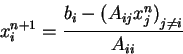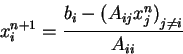Méthodes itératives

Ces méthodes utilisent un processus itératif pour obtenir la solution du système. Elle permettent d'utiliser des stockages dans lesquels seuls les termes non nuls sont stockés, elles conduisent à des occupations mémoire significativement plus petites que les méthodes directes et sont intéressantes pour traiter les problèmes ayant un très grand nombre d'inconnues. On donne, à titre d'exemple, le schéma de la méthode de Gauss-Seidel :

$$x^{n+1}_i = \frac{b_i - {(A_{ij} x^n_j)}_{j \neq i}}{A_{ii}}$$

Les méthodes itératives actuellement les plus utilisées sont les méthodes de type gradient conjugué ou GMRES.