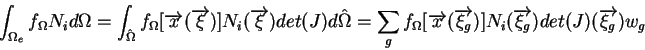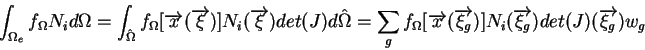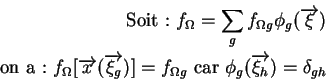Projection sur la base définie par l'intégration numérique

On a vu plusieurs projections des fonctions données (par noeud, par élément). Avec une méthode d'intégration on peut aussi procéder de la façon suivante :

$$\begin{eqnarray*}\int_{\Omega_e} f_\Omega N_i d\Omega = \int_{\hat{\Omega}} f_\O... ... N_i (\overrightarrow{\xi_g}) det(J)(\overrightarrow{\xi_g}) w_g \end{eqnarray*}$$

Ceci revient à utiliser une projection de 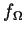$f_{\Omega}$ sur un espace d'approximation avec des fonctions 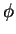$\phi$ définies sur les points de l'intégration numérique. C'est une approximation non conforme car les fonctions 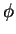$\phi$ ne sont pas continues aux frontières des éléments ; elles sont en effet définies par des points situés à l'intérieur des éléments. Cette approximation demande moins d'opérations que l'approximation nodale conforme.

$$\begin{eqnarray*}\mbox{Soit : } f_{\Omega} = \sum_g f_{\Omega g} \phi_g (\overri... ...ega g} \mbox{ car } \phi_g(\overrightarrow{\xi_h}) = \delta_{gh} \end{eqnarray*}$$